Statistik

• Maße
  • Mittelwert: $\bar{x} = \frac{1}{n} \sum_i^n x_i$
  • Stichprobe: $s_{xy} = \frac{1}{n - 1} \sum_i (x_i - \bar{x}) (y_i - \bar{y})$
  • Stichprobenvarianz $s_x^2 = \frac{1}{n - 1} \sum_i (x_ i - \bar{x})^2$
  • Varianz: $var(X) = E[(X - E(X))^2]$
  • Standardabweichung: $\sigma_X = s_X = \sqrt{var(X)}$
  • Kovarianz: $cov(X, Y) = E[(X - E(X)) (Y - E(Y))] = E(XY) - E(X)E(Y)$ (anderes Maß für Korrelation)
  • Pearsons Korrelationskoeffizienten $r = \frac{cov(X, Y)}{\sqrt{var(X) var(Y)}}, -1 \leq r \leq 1$
  • Empirischer Korrelationskoeffizient: $R = \frac{s_{xy}}{s_x s_y}$ (Schätzung für r)
• Regeln
  • $var(X) = cov(X, X)$
  • $var(X + Y) = var(X) + var(Y) + 2 cov(X, Y)$ (Kovarianz ist Ausgleichsterm für Additivität der Varianz)
• $r = 0 \Rightarrow$ X und Y unkorreliert, X und Y unabhängig $\Rightarrow r = 0$
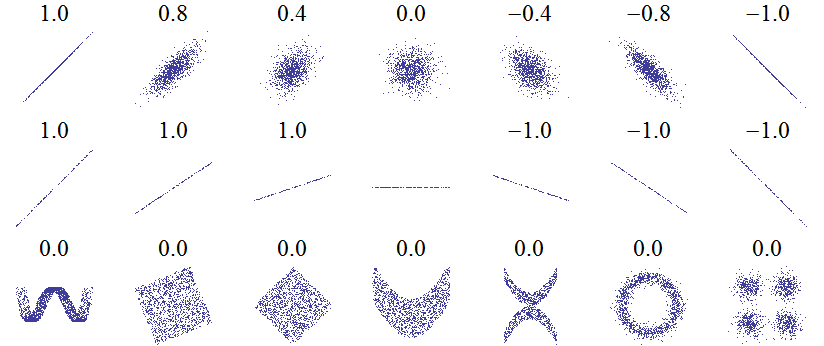
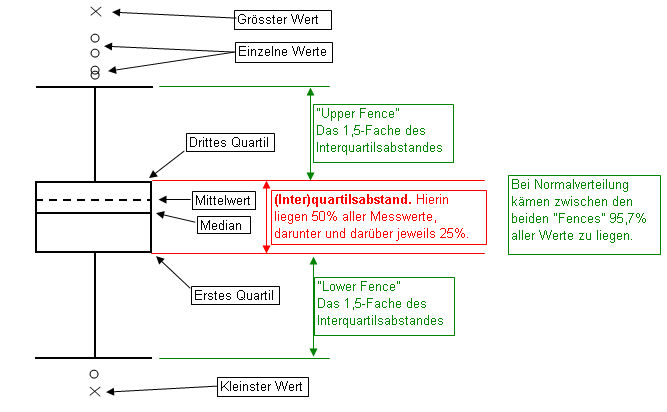
• Korrelation
  • R: (A+C) / (B+D) = R, hoch: R positiv, niedrig: R negativ
  • oder: A + D >> B + C: pos, B + C >> A + D (C | D, A | B)

Regressionsanalyse

$\hat{y} = b_0 + b_1 x_1 + \ldots + b_p x_p + e$

• y: abhängig, x: unabhängig, $b_i$: Modellparameter, e: Fehlervariable
• Annahmen: $e_n$ normalverteilt, $E(e_n) = 0, var(e_n) = \sigma^2, cov(e_m, e_n) = 0, m \neq n$
• Minimiere: $SAQ(b_0, b_1) = \sum_{i = 1}^N (y_i - b_0 - b_1 x_i)^2$
  • $b_0 = \bar{y} - b_1 \bar{x}, b_1 = \frac{\sum_{i = 1}^N x_i y_i - n \bar{x} \bar{y}}{\sum_{i = 1}^N x_i^2 - n \bar{x}^2}$
  • SQT: erklärende Abweichungen (SQE + SQR), SQE: erklärte, SQR: nichterklärte
• Bestimmtheitsmaß: $r^2 = \frac{SQE}{SQT}, SQE = \sum_{i = 1}^N (\hat{y}_i - \bar{y})^2, SQT = \sum_{i = 1}^N (y_i - \bar{y})^2$
  • 0: keine Erklärung, 1: vollständige Erklärung
• Lineare logistische Regression
  • abh. Variable Y ist binär
  • Rechne mit Wsk $p = P(Y = 1) \Rightarrow 0 \leq p \leq 1$
  • Betrachte Chance: $\frac{P(Y = 1)}{P(Y = 0)} = \frac{p}{1 - p}$
  • Logit-Funktion: $logit(p) = \ln(\frac{p}{1 - p}) = b_0 + b_1 X = z \Rightarrow p = \frac{e^z}{1 + e^z}$
  • nur approxmierbar (zB. Maximum-Likelihood)

Testverfahren

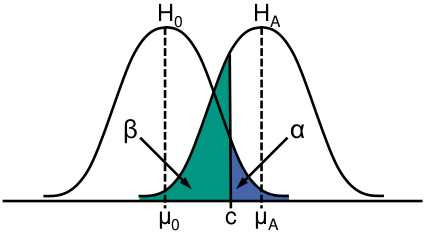
• Signifikanzniveau $\alpha$, krititscher Wert $c$, Effektgröße $\gamma$
• einseitig oder zweiseitig
• Vorgehen
  1. Aufstellung von $H_0$ und $H_A$ und Festlegung von $\alpha$
  2. Festlegung geeigneter Prüfgröße und Testverteilungsbestimmung
  3. Bestimmung des kritischen Bereichs
  4. Berechnung des Wertes der Prüfgröße
  5. Entscheidung + Interpretation
• Zusammenhänge
  • $\alpha+ \Rightarrow \beta-$ (höhere Güte)
  • $(\mu_0 - \mu_A)+ \Rightarrow \beta-$ (höhere Güte)
  • $n+ || \sigma^2- \Rightarrow (1 - \beta)+$
  • ES- $\Rightarrow$ Güte-
• t-Test
  • parametrisch, Gleichheit der Erwartungswerte
  • Voraussetzungen: Normalverteilung (Varianz unbekannt)
  • $T = \frac{\bar{X} - \mu_0}{S} \sqrt{n}$ (T Student-t-verteilt)
  • falls Varianz bekannt: $Z = \frac{\bar{X} - \mu_0}{\sigma} \sqrt{n}$
  • überschätzt / ist aggressiv
• F-Test für Gleichheit der Varianzen

Güteananalyse

• 4 Parameter: $\alpha, 1 - \beta, n, \gamma$ (aus 3 ist der 4. berechenbar)
  • n: vor Expirement, ES schätzen mit Pilotstudie / vergl. Expiremnt, Grundlage für Hypothesentest
  • Güte: für Korrekturen am Expirementaufbau (=Wsk selbes Ergebnis)
  • ES: Maß für Vergleich von Studien ($\gamma = \frac{\mu_x - \mu_y}{\sigma}$, 0.2(klein), 0.5(mittel), 0.8 (groß))
  • $\alpha$: ungewöhnlich (meist n und Güte)
• Standardwerte: $\alpha = 0.05, \beta = 0.2$ (+schätze ES --> berechne n)
• Auswertung: nur falls Hypothese nicht abgelehnt (bei geringer Güte wird kleiner Effekt angenommen)
• Probleme
  • Overpowered: zu viele Daten --> kleine, uninteressante Effekte haben Einfluss
  • Underpowered: zu wenige Daten --> Effekt nur mit geringer Wsk zeigbar
• Wilcoxon-Test braucht im wc $\frac{1}{0.864}$ mehr Datenpunkte als t-Test (selbe Güte)

Wilcoxon-Rangsummentest

• nicht parametrisch (keine Ann. über Parameter der Verteilung), Zweistichproben-Test, Gegenstück zum t-Test
  • Überprüfung ob Stichproben selbe Verteilung besitzen (keine Normalverteilungsannahme)
• Voraussetzungen: X, Y unab., haben stetige Verteilungsfunktionen F, G
  • Hypothesen: $H_0: F(z) = G(z), H_1: \forall z \in R, \theta \neq 0: F(z - \theta) = G(z)$
  • F, G selbe Form, aber mögl. verschoben
  • F, G normalverteilt --> t-Test (Erwartungswert) + F-Test (Varianz)
• Vorgehen
  1. Beob. X (Länge m), Y (Länge n), $m \leq n, N = m + n$
  2. Kombiniere Stichproben + sortiere
  3. Vergebe Ränge 1 bis N (bei gleichem Wert, verwende Mittelwert)
  4. Summiere die Ränge von X: $W_N = \sum_{i = 1}^{N} i V_i$
  5. Wähle $\alpha$ + Teste $H_0$: lehne ab, falls $W_N \leq w$ (je nach ein- oder zweiseitiger Test)